拉格朗日乘数法

By Z.H. Fu https://fuzihaofzh.github.io/blog/ 　　拉格朗日乘数法在优化理论中起着非常重要的作用。本文将给出拉格朗日乘数法的具体步骤和一个直观的理解。

拉格朗日乘数法解决这样一个问题：
　　
　　$$\begin{cases}maximize\quad &f(x,y) \ subject \quad to\quad &g(x,y)=c\end{cases}$$
　　我们在等高线图上考虑，先任取$f(x,y)=d_2$此时，等高线与约束线的交点既是满足约束且取值为$d_2$的点。下面，我们逐渐增大$f(x,y)$的取值，即$d$逐渐由$d_2$变为$d_1$，这个过程中，$f(x,y)$的值逐渐增大，当达到$d_1$后，再增大一点点，即不满足约束，因此$d_1$既是$f(x,y)$在该约束下的最大值。而这个时候，约束曲线正好和等高线相切。既是说，在这一点，$f(x,y)$和$g(x,y)$的梯度方向相同，拉格朗日乘数法即是刻画了梯度方向相同这一特点。我们能找到一个标量$\lambda$使得：　　$$\nabla f+\lambda \nabla g=0 $$
　　
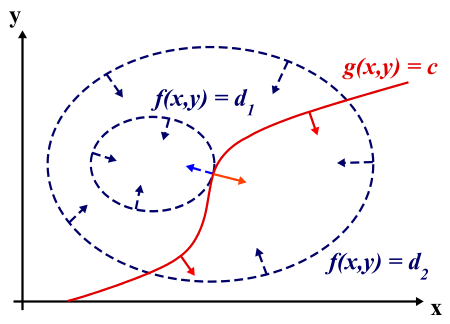
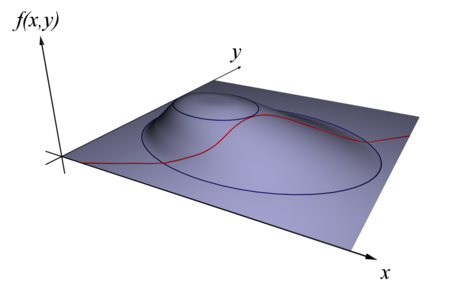
　　以下给出更规范的描述。
　　令拉格朗日函数
　　$$\Lambda(x,y,\lambda)=f(x,y)+\lambda (g(x,y)-c)$$
　　优化问题取得最大值，等价于拉格朗日函数取得驻点。即：
　　$$\nabla_{x,y,\lambda}\Lambda=0$$
　　这样，就将一个带约束优化问题，转化成了一个无约束的极值问题。

参考文献

[1]拉格朗日乘数 https://zh.wikipedia.org/wiki/拉格朗日乘数

[2]Lagrange multiplier https://en.wikipedia.org/wiki/Lagrange_multiplier