仿射空间与仿射变换

By Z.H. Fu https://fuzihaofzh.github.io/blog/ 　　　　　　 ## 为什么需要仿射变换？　　

仿射空间与仿射变换在计算机图形学中有着很重要的应用。在线性空间中，我们用矩阵乘向量的方法，可以表示各式各样的线性变换，完成诸多的功能，但是有一种极其常用的变换却不能用线性变换的方式表示，那就是平移，一个图形的平移是非线性的！（这一点只需要看平移前各点与原点的连线和平移后各点与原点之间的连线可知，或者记平移变换为$\mathcal{F}$，有$\mathcal{F}(\boldsymbol{v_1}+\boldsymbol{v_2})\not =\mathcal{F}(\boldsymbol{v_1})+\mathcal{F}(\boldsymbol{v_2}))$

放射空间与仿射组合

为了用数学的方式来描述这种变换，就需要用到仿射变换（平移不是线性变换而是仿射变换）。下面先讲仿射空间。形象地来讲，仿射空间就是没有原点的线性空间。在线性空间中，两个点相加，可以定义为原点到两个点的向量线性相加，而在仿射空间中，由于没有原点，因此不能定义相加，没有线性组合。但我们可以定义一个仿射组合来用若干基表出某个点。我们定义仿射组合：

$$\boldsymbol{p}=\sum_{i=1}^N \lambda_i \boldsymbol{v_i}\quad\quad(\sum_{i=1}^N \lambda_i=1)$$

我们不妨在线性空间中来看这个式子，假设就两个向量$\boldsymbol{v_1,v_2}$我们任意指定一个原点$\boldsymbol{q}$，设$\boldsymbol{v_1}$的系数为$\lambda$，则$\boldsymbol{v_2}$的系数为$1-\lambda$，那么$\boldsymbol{p}=\boldsymbol{q}+\lambda(\boldsymbol{v_1}-\boldsymbol{q})+(1-\lambda)(\boldsymbol{v_2}-\boldsymbol{q})=\lambda \boldsymbol{v_1}+(1-\lambda)(\boldsymbol{v_2})$。通过推导，原点$\boldsymbol{q}$被消去了，也就是说，仿射组合跟原点的选择没有任何关系！

仿射变换

有了仿射组合，就可以仿照线性组合来定义仿射变换：

给定两个仿射空间$\mathcal{A},\mathcal{B}$，一个函数$f:\mathcal{A}\rightarrow \mathcal{B}$是仿射变换，当且仅当对仿射组合

\sum_{i=1}^N \lambda_i \boldsymbol{v_i}\quad\quad(\sum_{i=1}^N \lambda_i=1)$$都有 $$f(\sum_{i=1}^N \lambda_i \boldsymbol{v_i})=\sum_{i=1}^N \lambda_if(\boldsymbol{v_i})\quad\quad(\sum_{i=1}^N \lambda_i=1)

这种系数又叫质心坐标，哪个点的系数大，就相当于质量大，质心就离那个点近。仿射变换得到的结果就是给定点按质量加权的质心，质心的仿射变换等于每个点进行放射变换后再求质心。

用线性变换表示仿射变换

下面来看如何表示仿射变换，我们定义$\mathbb{R}^n$中一个向量$\boldsymbol{v}$的齐次形式为$\mathbb{R}^{n+1}$中的$\overset{\sim}{\boldsymbol{v}}=\left[\begin{aligned}\boldsymbol{v} \\ 1\end{aligned}\right]$那么，仿射组合与系数和为1的要求可统一表示为

$$\left[\begin{aligned}\boldsymbol{y} \\ 1\end{aligned}\right]=c_1\left[\begin{aligned}\boldsymbol{v_1} \\ 1\end{aligned}\right]+c_2\left[\begin{aligned}\boldsymbol{v_2} \\ 1\end{aligned}\right]+\cdots+c_n\left[\begin{aligned}\boldsymbol{v_n} \\ 1\end{aligned}\right]$$

也就是说，仿射组合可以写成高一维对应齐次坐标的线性组合形式。那么对于一个附加平移的变换

$$\boldsymbol{y}=A\boldsymbol{x}+\boldsymbol{b}$$

我们可以将其改写成其次坐标的形式

\left[\begin{aligned}\boldsymbol{y} \\ 1\end{aligned}\right]=\left[\begin{aligned}&A &\boldsymbol{b} \\ &0 &1\end{aligned}\right]\cdot\left[\begin{aligned}\boldsymbol{x} \\ 1\end{aligned}\right]$$这也是在计算机图形学中对平移的处理方式。下面一个摘自维基百科的图形象地说明了这一过程 <center>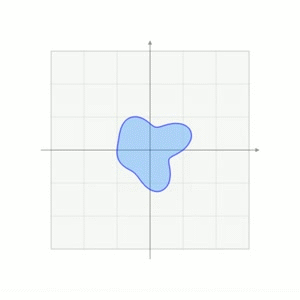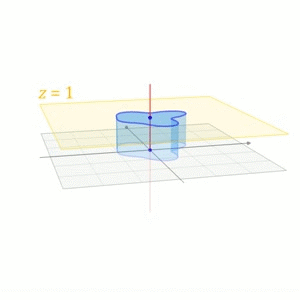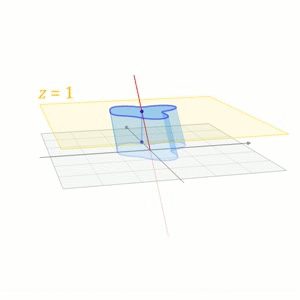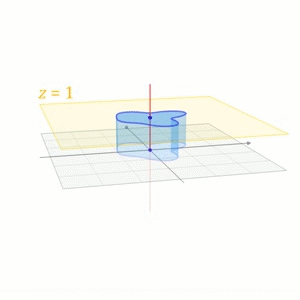</center> 　　　　　　　　　　 ## 其它 　　我们再来看看质心坐标（Barycentric Coordinates），采用质心坐标的好处在于它能够表示每一点受周围点的影响，质心坐标的系数越大，影响越大，因此在线性插值时，可以直接用质心坐标来乘以每一点的值，得出的就是插值后的结果，在计算机图形学中进行渲染时，颜色差值就用这种算法。 　　　　　　　　　　　　　　　　　　 ## 参考文献 [1]D C.Clay Linear Algebra and its application 4th edition [2]http://en.wikipedia.org/wiki/Affine_space [3]http://en.wikipedia.org/wiki/Affine_transformation