By Z.H. Fu
https://fuzihaofzh.github.io/blog/
组合数是排列组合中最基础的一个公式,本文首先给出组合数公式的一个直观理解,并将其推广为多分组公式。
组合数定义为:
$$\binom{n}{k}=\frac{n!}{k!(n-k)!}$$
一般对这个公式的理解是从$n$个物品中选取$k$个物品的方法数,在这里我们从另一个角度来理解这个公式:将n个物品分为两堆,一堆$k$个,一堆$n-k$个,一个直观的示意图如下图所示
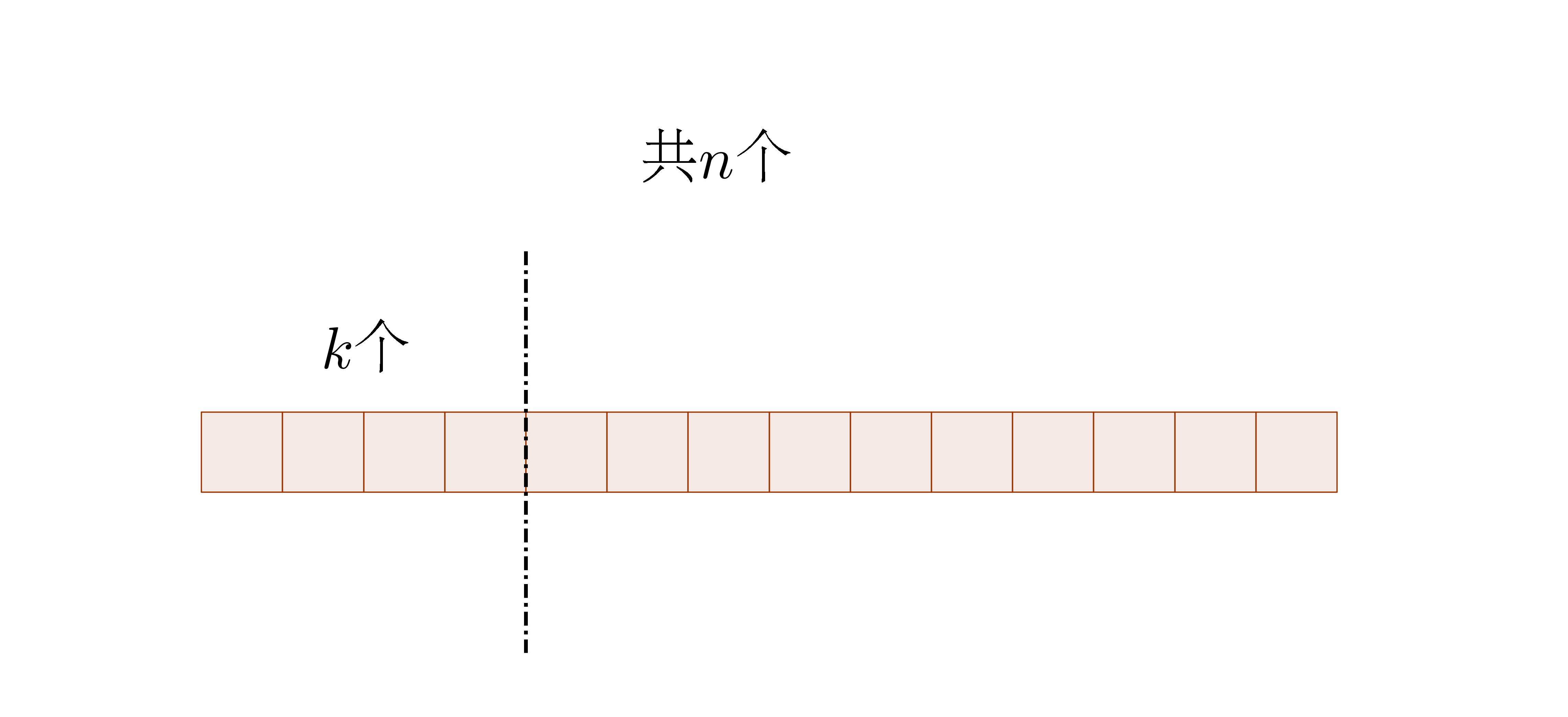
在这里,$n!$表示将$n$个物品一个一个地放入格子中,第一个物品有$n$种选择,第二个物品有$n-1$种选择,以此类推。这样,两堆就分好了,但是要注意到的是,这里的分堆是与顺序无关的,因此要分别除以没一堆的全排列个数,这样就得到了总的分堆方法。
那么自然地,我们可以将上面的概念推广到$m$堆的情况,即求$n$个物品,分入$m$堆中,每一堆的个数分别为$k_1,k_2,\cdots,k_m$,那么总的分类个数有
$$\frac{n!}{k_1!k_2!\cdots k_m!}$$
示意图如下:
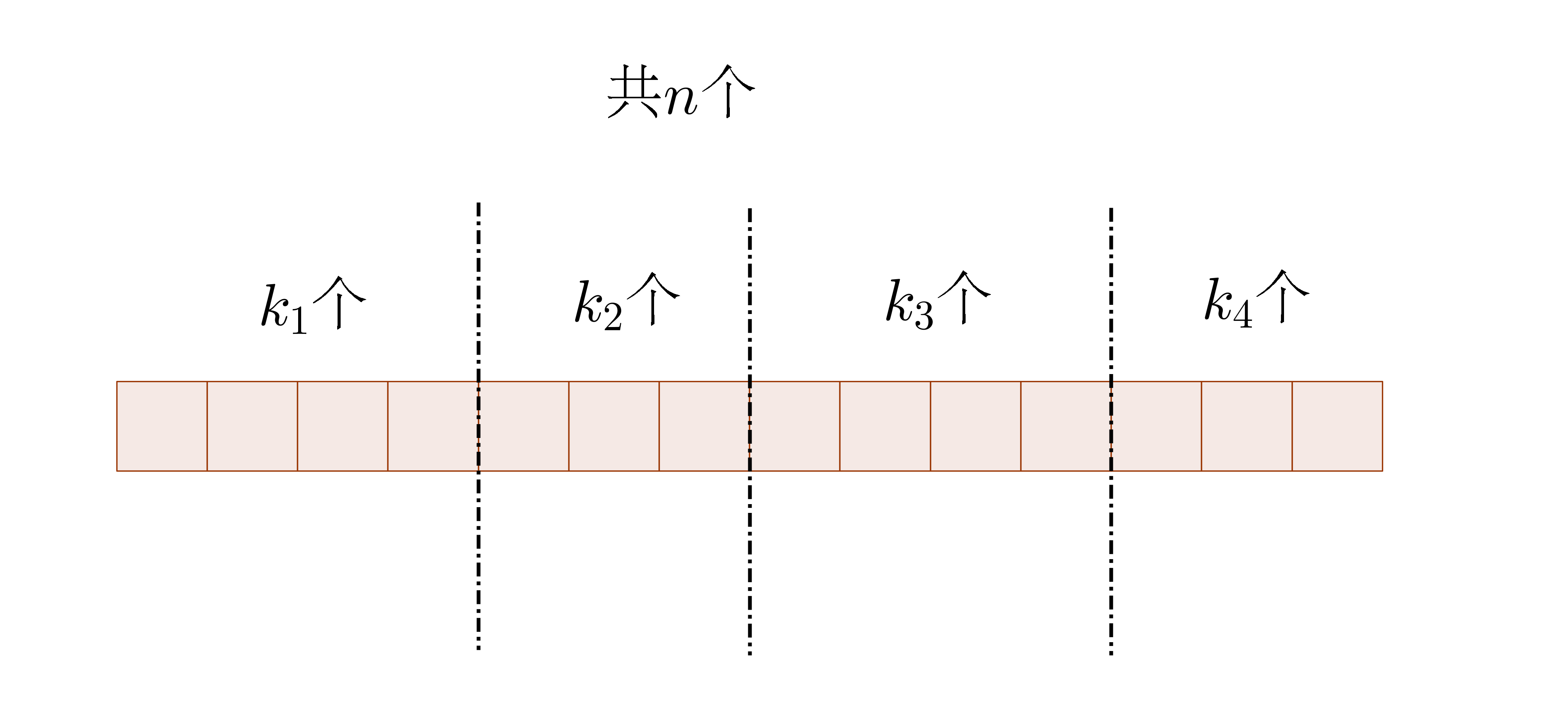
我们仿照组合数的定义,给出多分类的组合数,有:
$$\binom{n}{k_1!k_2!\cdots k_m!}=\frac{n!}{k_1!k_2!\cdots k_m!}$$
类似于二项式系数,这个组合数也叫做多项式系数,可用于表示多项式展开后各项的系数情况,我们讲一个多项式展开,其中每一项的系数就等于多项式系数,有:
$$(x_1+x_2+\cdots +x_m)^n=\sum_{k_1+k_2+\cdots k_m=n}\binom{n}{k_1!k_2!\cdots k_m!}x_1^{k_1}x_2^{k_2}\cdots x_m^{k_m}$$
即是说,$\binom{n}{k_1!k_2!\cdots k_m!}$就是多项式$(x_1+x_2+\cdots +x_m)^n$展开后,$x_1^{k_1} x_2^{k_2}\cdots x_m^{k_m}$那一项的系数。
参考文献
[1] 概率与数理统计 陈希孺