一个集合和其全子集一定不是等势的证明

By Z.H. Fu https://fuzihaofzh.github.io/blog/ 这里主要证明一个集合一定不能与其所有子集等势，即建立集合的一一对应关系。 我们记集合为$X$，相应地，其所有子集构成的集合记作$2^X$，我们用反证法。 首先，假设$X$和$2^X$存在一一映射$f:X\rightarrow 2^X$，那么$\exists A=\{A \subset X|x \in A, x \notin f(x)\}$，这里解释下符号，$x$是$X$中的一个元素，其在$2^X$中的象为$f(x)$，而$A$是$X$的一个子集(用符号表示就是$A \subset X,A \in 2^X$)，该子集中的每一个元素的象都不包含自己。那么，我们对于$2^X$中元素$A$的原象$x$，若$x \in A$，那么$x \notin f(x)$即$x \notin A$，矛盾；若$x \notin A$，那么$x \in f(x)$即$x \in A$矛盾。综上集合不能与其自身所有子集等势。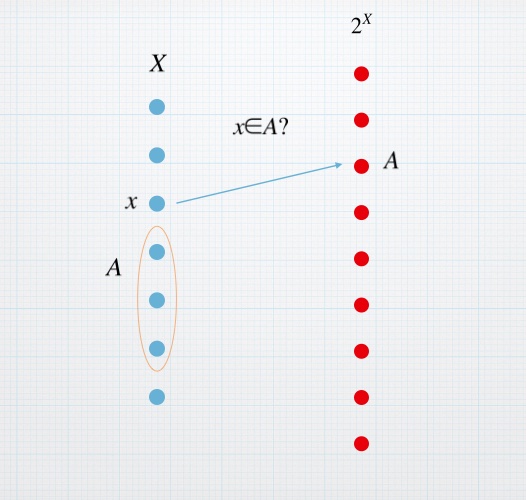  注意，这个的证明和罗素悖论的证明非常相似。