理解PCA和SVD

By Z.H. Fu https://fuzihaofzh.github.io/blog/ ## 摘要 本文主要从分解形式上讲述了PCA（Principal Component Analysis，主成分分析）和SVD（Singular Value Decomposition奇异值分解）的目的和方法，对于两种方法都给出了一种直观的理解。简单起见，本文不给出具体的应用实例。 ## PCA 主成分分析（PCA）常用于提取一系列多维样本的共同特征。那么，怎么理解特征？我们假设每个样本是由一系列的特征线性组合而成的，PCA的目的就是去找到这些特征，然后将每一个样本表示为这些特征的组合，实际上PCA找到了样本空间中的一组基，将每一个样本表示为这组基的线性组合，因此，每一个基就是一个特征。那么，特征需要满足哪些性质呢？其实就一点，特征之间的关系应该越少越好。用基来描述就是这应该是一组正交基。下面我们来看该怎么构造这组基。  我们假设我们的样本矩阵为$A_{m\times n}$每一行为一个样本，共m个样本，每一列是一个特征，共n个特征。我们来看怎么刻画特征不相关这个事情。我们可以看两个随机变量不相关是怎么刻画的，两个随机变量不相关，即他们的协方差为0，即： $$cov(X,Y) = E([X-E[X]][Y-E[Y]) = 0$$ 这启发我们，能不能通过某个线性变换，将样本矩阵变换为一个新矩阵，让新矩阵的每一列不相关，那么为了表示矩阵每一列不相关这个事，我们要先做一个简化，先来考虑均值为0的两个随机变量$X,Y$，那么他们的协方差可表示为： $$cov(X,Y) = E([X-0][Y-0]) = E(XY)$$ 即点乘为0，因此我们先求出每一列的均值并将均值归为0（即每一列的所有元素减去当前列的均值）。这样矩阵A通过某个线性变换得出的新矩阵B的每一列都正交，用矩阵表示即为： $$B^TB=D$$ 其中，D是一个对角阵。 那么我们假设这个变换是$AM=B$，将这个带入得： $$\begin{align} (AM)^T(AM)=D \\ M^TA^TAM=D \\ A^TA=(M^T)^{-1}DM^{-1} \end{align}$$ 而我们知道$A^TA$是一个对角阵，那么它的特征值分解$A^TA=VDV^{-1}$中的V是正交单位阵，那么有$V^T=V^{-1}$，那么这个V就满足我们对M的要求。 所以，我们对矩阵A做PCA的步骤就是：

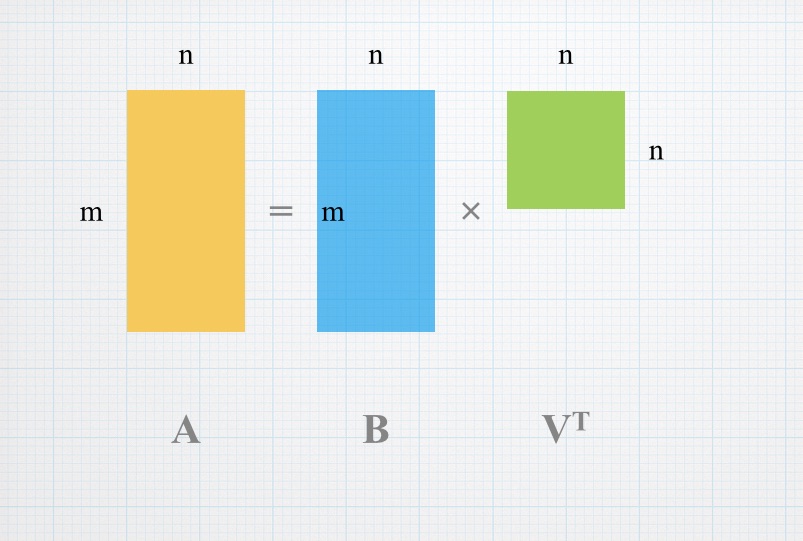
1.将A的每一列按均值做归一化，使归一化后的A的每一列均值为0；
2.求出$A^TA$的特征值$D=diag\{\lambda_1,\lambda_2,\cdots,\lambda_n\}$和特征矩阵V；
3.令矩阵$B=AV$。

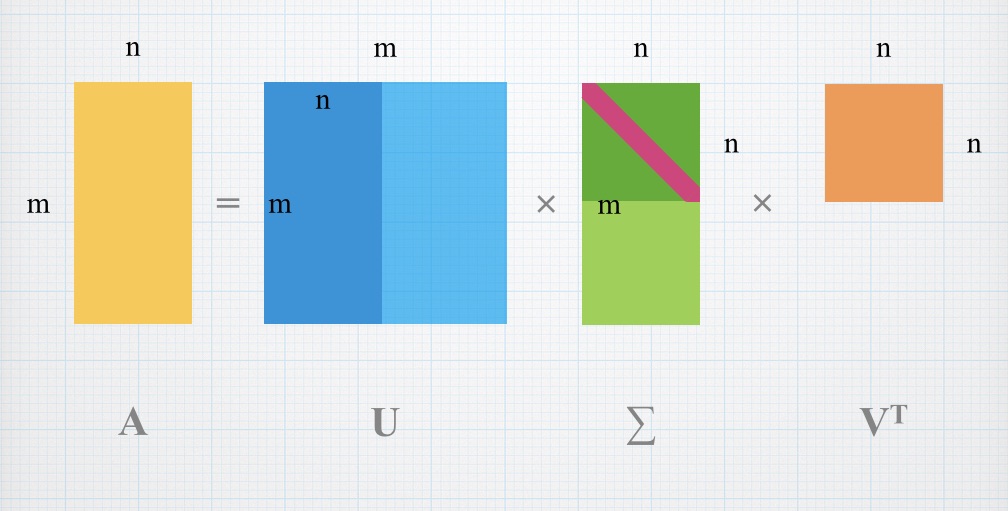
这个矩阵B就是我们需要的新矩阵，它的每一列均值为0，且每一列正交，而$A=BV^T$其中，$V^T$的每一行就是我们想要的特征，B的每一行就是特征的组合系数。

SVD

SVD（Singular Value Decomposition奇异值分解）是一种矩阵分解的方法，目的很明确，就是将矩阵A分解为三个矩阵$U\Sigma V^T$的乘积的形式，我们不妨接着PCA的步骤往下做。
我们有$A=BV^T$，我们将B写成归一化的形式，其拆开成$B=U\Sigma$，其中U的每一列是单位向量，而$\Sigma=diag\{\sigma_1,\sigma_2,\cdots,\sigma_n\}$则是B中每个向量的模长且$\sigma_1>\sigma_2>\cdots>\sigma_n$。而B中每一列的模长为$Av_i$，由于$v_i$是$A^TA$的特征向量，对应特征值为$\lambda_i$，那么$Av_i$平方为

\begin{align} (Av_i)^TAv_i & = (Av_i)^TAv_i \\ & = v_i^TA^TAv_i \\ & = v_i^TA^TAv_i \\ & = v_i^T\lambda_iv_i \\ & = \lambda_iv_i^Tv_i \\ & = \lambda_i \\ \end{align}

所以有$|Av_i|=\sqrt{\lambda_i}$，所以将B写成$B=U\Sigma$的形式后，U是正交矩阵，而$\Sigma$是一个对角阵，其每一个元素$\sigma_i=\sqrt{\lambda_i}$。
我们再来看SVD的图示：

从图中看出，中间的奇异值矩阵由大到小排列，越后面的值对结果的影响越小，因此，如果只保留较大的奇异值和其对应的U、V中的向量，对于矩阵压缩则能起到很好的作用。在该例子中，$m>n$，能通过$u_i=\frac{Av_i}{\sigma_i}$得出的$u_i$只有n个，剩下m-n个基直接随便找正交基补全即可，他们在计算中实际上也没什么用。
我们把SVD分解的结果带入协方差矩阵：

$$A^TA=(U\Sigma V^T)^TU\Sigma V^T=V\Sigma U^TU\Sigma V^T=V\Sigma^2 V^T$$

可以看出，中间那个U消掉了，这也能部分反映SVD和PCA间的关系。

参考文献

[1] http://www.math.umn.edu/~lerman/math5467/svd.pdf