矩阵的条件数是什么

By Z.H. Fu https://fuzihaofzh.github.io/blog/

条件数定义

在矩阵的数值计算中经常会遇到条件数的概念，条件数通常用于描述一个线性系统的稳定性，条件数越大，系统的稳定性越差。通常条件数太大的线性系统，求得的解会受到舍入误差的严重影响。下面我们来看条件数的一些概念。

条件数被定义为：

$$\kappa (A)=||A||_2||A^{-1}||_2$$

其中，$||A||_2$表示矩阵的二范数，定义为：

$$||A||_2=\max_{x \neq 0 }\frac{||Ax||_2}{||x||_2}$$

因此，条件数可表示为：

$$\kappa(A)=||A||_2||A^{-1}||_2=\left(\max_{x \neq 0 }\frac{||Ax||_2}{||x||_2}\right)\left(\min_{x \neq 0 }\frac{||Ax||_2}{||x||_2}\right)^{-1}$$

可以看出，他的意义就是单位向量拉伸的最大比例除以单位向量拉伸的最小比例。而这个拉伸比例就是矩阵最大和最小的奇异值，记作$\sigma_n(A),\sigma_1(A)$有

$$\kappa(A)=\frac{\sigma_n(A)}{\sigma_1(A)}$$

条件数与奇异值

我们再来回顾一下奇异值分解（参见 理解PCA和SVD ），矩阵$A$的奇异值分解为$A=U\Sigma V^T$，其中，$U,V$为正交单位阵，因此$Ax=U\Sigma V^Tx=U\Sigma y$，这里$y = V^Tx$是对$x$做一个正交变换，其模长不变，若$x$为单位向量的话，$y$也为单位向量。同理最后用$U$来对$\Sigma y$进行正交变换也不改变其模长，因此，最终的模长可看做是一个对角阵$\Sigma$对一个单向量$y$，进行变换的结果，而对角阵$\Sigma$的对角元素就是奇异值，如果最大的奇异值和最小的奇异值相差较大的话，那么对一个单位向量的变换结果模长的变化范围就很大，这样的话，不同向量的计算出的数量级不一样，就会出现舍入误差的问题。


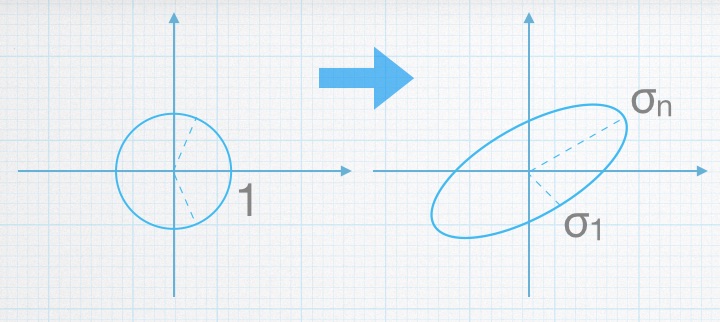
通过上图中我们也能看出，奇异值相差越大，椭圆的长短半轴差异就越大，就越接近于一个奇异矩阵，当最小奇异值有0存在时，条件数变为正无穷，是个奇异矩阵。

举一个简单的例子

$$\begin{bmatrix} 1 & 1 \\ 1 & 1.001 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}= \begin{bmatrix} 2 \\ 2 \end{bmatrix}$$

其解为$\begin{bmatrix} 2 \\ 0 \end{bmatrix}$

而

$$\begin{bmatrix} 1 & 1 \\ 1 & 1.001 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}= \begin{bmatrix} 2 \\ 2.001 \end{bmatrix}$$

其解为$\begin{bmatrix} 1 \\ 1 \end{bmatrix}$

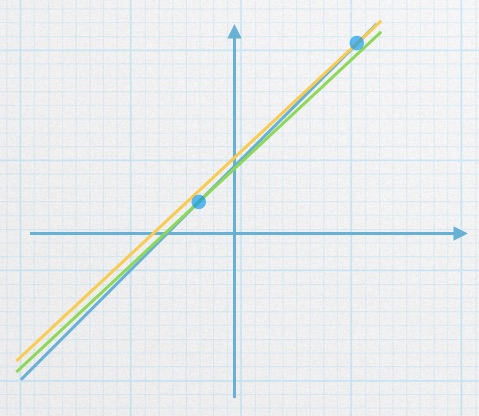
右边项改变一小点，将造成解差很多，这个从下面的图示中也能看出，黄线与绿线平行，绿线比黄线只平移了一点，但是与蓝线的交点差异很大。这说明，输入的一点误差将引起输出解得巨大变化。这种系统是在设计中应该尽量避免的。


参考文献

[1] http://www.fuzihao.org/blog/2015/12/04/理解PCA和SVD/
[2] http://www.math.pitt.edu/~sussmanm/2071Spring09/lab05/

[3] http://120.52.72.48/www.cs.yale.edu/c3pr90ntcsf0/homes/spielman/BAP/lect2.pdf

[4] http://www.cse.iitd.ernet.in/~dheerajb/CS210_lect07.pdf