Predict Time Sequence with LSTM

By Z.H. Fu https://fuzihaofzh.github.io/blog/ In this article, we try to use LSTM to learn some sine waves and then to draw the waves all by itself.  ## introduction RNN(Recurrent Neural Network) is a kind of neural network which will send current information recurrently back to itself. As a result, it can "remember" something of previous samples. However common RNN can not remember too much things because of the gradient vanishing problems. When error back propagates to the previous layers, it will multiply the gradient of the activation function which is less than 1. After several steps, it decays to nearly 0. LSTM(Long Short Term Memory)[1] is one kind of the most promising variant of RNN. Some gates are introduced into the LSTM to help the neuron to choose when to forget and when to remember things. It tackle the gradient vanishing problems with some more parameters introduced. Here we use a sine wave as input and use LSTM to learn it. After the LSTM network is well trained we then try to draw the same wave all by LSTM itself. ## construct the LSTM in Theano

There are a lot of deep learning framework we can choose such as theano, tensorflow, keras, caffe, torch, etc. However, we prefer theano than others because it gives us the most freedom to construct our programs. A Library called Computation Graph Toolkit is also very promising but it still need some time to become user friendly. The theano tutorial is offered in [2].

Firstly we construct the LSTM kernel function according to [3]. The LSTM function is a bit more complicated than traditional RNN with three more gates. The function is defined as:

def lstm(x, cm1, hm1, ym1, W):
    hx = T.concatenate([x, hm1])
    hxSize = hx.shape[0]
    bs = 0
    Wf = W[bs: bs + hiddenSize * hxSize].reshape([hiddenSize, hxSize])
    bs += hiddenSize * hxSize
    bf = W[bs: bs + hiddenSize]
    bs += hiddenSize
    Wi = W[bs: bs + hiddenSize * hxSize].reshape([hiddenSize, hxSize])
    bs += hiddenSize * hxSize
    bi = W[bs: bs + hiddenSize]
    bs += hiddenSize
    Wc = W[bs: bs + hiddenSize * hxSize].reshape([hiddenSize, hxSize])
    bs += hiddenSize * hxSize
    bc = W[bs: bs + hiddenSize]
    bs += hiddenSize
    Wo = W[bs: bs + hiddenSize * hxSize].reshape([hiddenSize, hxSize])
    bs += hiddenSize * hxSize
    bo = W[bs: bs + hiddenSize]
    bs += hiddenSize
    Wy = W[bs: bs + vectorSize * hiddenSize].reshape([vectorSize, hiddenSize])
    bs += vectorSize * hiddenSize
    by = W[bs: bs + vectorSize]
    bs += vectorSize

    ft = T.nnet.sigmoid(Wf.dot(hx) + bf)
    it = T.nnet.sigmoid(Wi.dot(hx) + bi)
    ct = T.tanh(Wc.dot(hx) + bc)
    ot = T.nnet.sigmoid(Wo.dot(hx) + bo)
    c = ft * cm1 + it * ct
    h = ot * T.tanh(c)
    y = Wy.dot(h) + by
    return [y, c, h, y]

We compact all parameters in W, and in the function we will unzip them respectively. x is the input vector of each step. cm1 is the memory state, hm1 is the hidden cell and y is the output. And then, we use Theano’s scan function to do a loop:

tResult, tUpdates = theano.scan(lstm,
                                outputs_info = [None,
                                        T.zeros(hiddenSize),
                                        T.zeros(hiddenSize),
                                        T.zeros(vectorSize)],
                                sequences = [dict(input = tx)],
                                non_sequences = [tW])

We define the loss as the square sum of the difference between output and the next x. So the input data is x[:-1] and the expected result is x[1:].

predictSequence = tResult[3]
tef = T.sum((predictSequence - ty)**2)
GetPredict = theano.function(inputs = [tW, tx], outputs = predictSequence)
GetError = theano.function(inputs = [tW, tx, ty], outputs = tef)
GetGrad = theano.function(inputs = [tW, tx, ty], outputs = tgrad)

After that, we use Adagrad to do the optimization. Adagrad is a simple and efficient optimization method which does better than L-BFGS(not faster than but get better result) and SGD. The Adagrad code is as follows:

for i in xrange(1000):
    dx = GetGrad(W, x, y)
    cache += dx**2
    W += - learning_rate * dx / (np.sqrt(cache) + eps)

However, LSTM is hard to optimize without some tricks. We introduce two tricks here. One is called weighted trainning and the other is denoising.

weighted trainning method

weighted trainning method weighted each step in the input sequence. Because we believe that the early stage of a sequence. Some small difference happened in the early stage will be broadcast in the following steps and will finally cause the prediction to fail. We can add a decaying weight to the sequence. It turned out to help a lot in the performance of the result. The result is shown as follows:

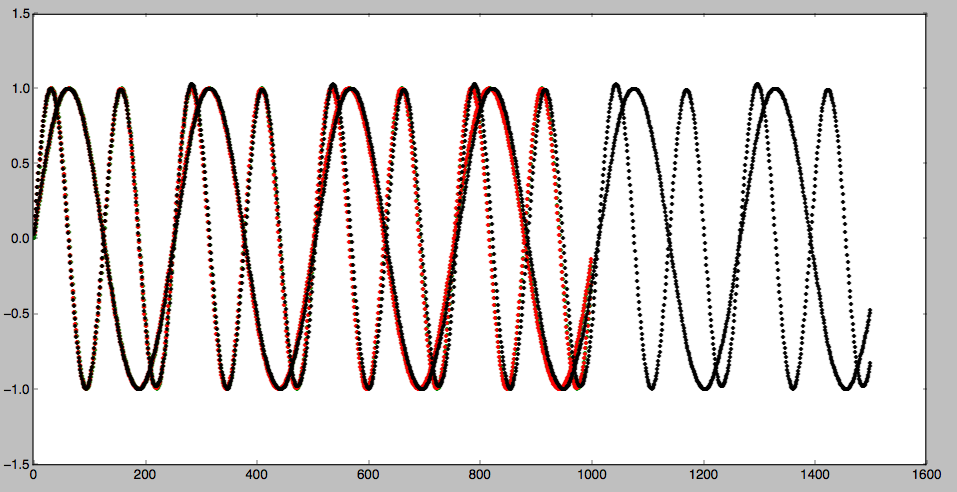
denoising LSTM

Another method, borrowed from denoising autoencoder is to add some noise to the sequence input. It can also help train the network. Besides, it needs less manipulation compared with the weighted methods. The result is shown as follow:

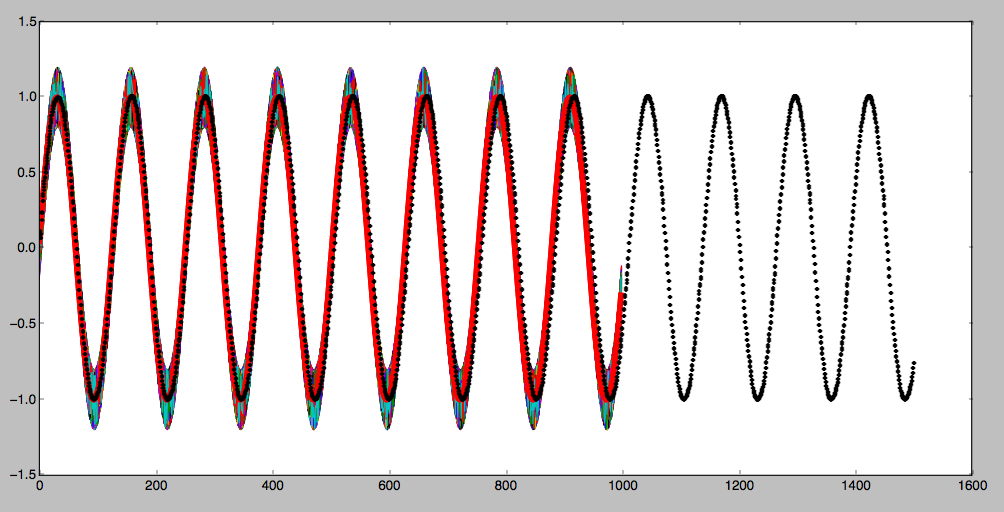
Conclusion

In this article, we do experiments on LSTM to predict the sequence itself. We tried weighted training method and denoising LSTM and the later one turn out to be more efficient.

Update: 2017/4/8

Code

The code was re-organised and re-written in pytorch and this example was adopted as one of the example of pytorch. This code can be downloaded at
https://github.com/pytorch/examples/tree/master/time_sequence_prediction

please contact me, if you have any question or some new ideas.

References
[1] Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780.
[2] http://deeplearning.net/software/theano/
[3] http://colah.github.io/posts/2015-08-Understanding-LSTMs/