切问录
0%

Sparse Fine-tuned Model -- An Unified View of Parameter-Efficient Models

Posted on Edited on Disqus:
Symbols count in article: 1.2k Reading time ≈ 4 mins.
By Z.H. Fu
https://fuzihaofzh.github.io/blog/

In the realm of machine learning, fine-tuning pre-trained models is a common practice. However, it often requires a significant amount of parameters and computational resources. To address this, researchers have proposed various parameter-efficient models, each with their own unique approach to fine-tuning. In this blog post, we will be discussing a unified view of these models, focusing on how they align with the definition of a sparse fine-tuned model. This view is a brief explanation of the study “On the effectiveness of parameter-efficient fine-tuning” by Zihao Fu et al. [1], can provide a unified understanding of parameter-efficient models and can be instrumental in further analysis and research.

What is a Sparse Fine-tuned Model?

A sparse fine-tuned model refers to a fine-tuned model that shares the same structure as the pre-trained model, with a certain level of sparsity in the difference of their parameters. More formally, it is defined as follows:

Definition(Sparse Fine-tuned Model) given a pre-trained model M0M^0 with parameters θ0\theta^0, if a fine-tuned model MM with parameters θ\theta shares the same structure as M0M^0 such that ∥θ−θ0∥0≤pdim⁡(θ),p∈(0,1)\|\theta-\theta^0\|_0\le p\dim(\theta),p\in(0,1), we say the model MM is a pp-sparse fine-tuned model with the sparsity pp.

This concept of sparsity is used to represent the degree of change between the pre-trained model and the fine-tuned model. A sparser model indicates a smaller degree of change, which can lead to more efficient usage of parameters.

Parameter-Efficient Fine-tuning Models

This paper [1:1] have categorized parameter-efficient fine-tuning models into three main categories: random approaches, rule-based approaches, and projection-based approaches. Each of these categories has a unique approach towards parameter selection, but all of them ultimately align with the definition of a sparse fine-tuned model. Let’s dive into each of these categories.

Random Approaches

Models in this category, such as Random and Mixout, randomly select parameters to be fine-tuned.

The Random model is straightforward - it selects parameters randomly with respect to a given sparsity ratio and then trains the selected parameters. As the selection does not depend on any specific data or rules, it complies with the definition of a sparse fine-tuned model.

The Mixout [2] model , on the other hand, proposes to directly reset a portion of the fine-tuned model’s parameters to the pre-trained parameters with respect to a ratio. This approach also aligns with the definition of a sparse fine-tuned model as it maintains a certain level of sparsity in the parameter changes.

Rule-Based Approaches

Rule-based approaches, such as BitFit, MagPruning, Adapter, and LoRA, use predefined rules to select parameters for fine-tuning.

The BitFit [3] model is a prime example of a rule-based approach. It only fine-tunes the bias-terms and achieves considerably good performance. This approach of pre-defining the weights to be tuned aligns with the definition of a sparse fine-tuned model.

The MagPruning [4] model follows the idea that large weights are more important in the model. It ranks the weights by the absolute value and tunes the parameters with high absolute values. This model also complies with the definition of a sparse fine-tuned model as it maintains a certain level of sparsity in the parameter changes.

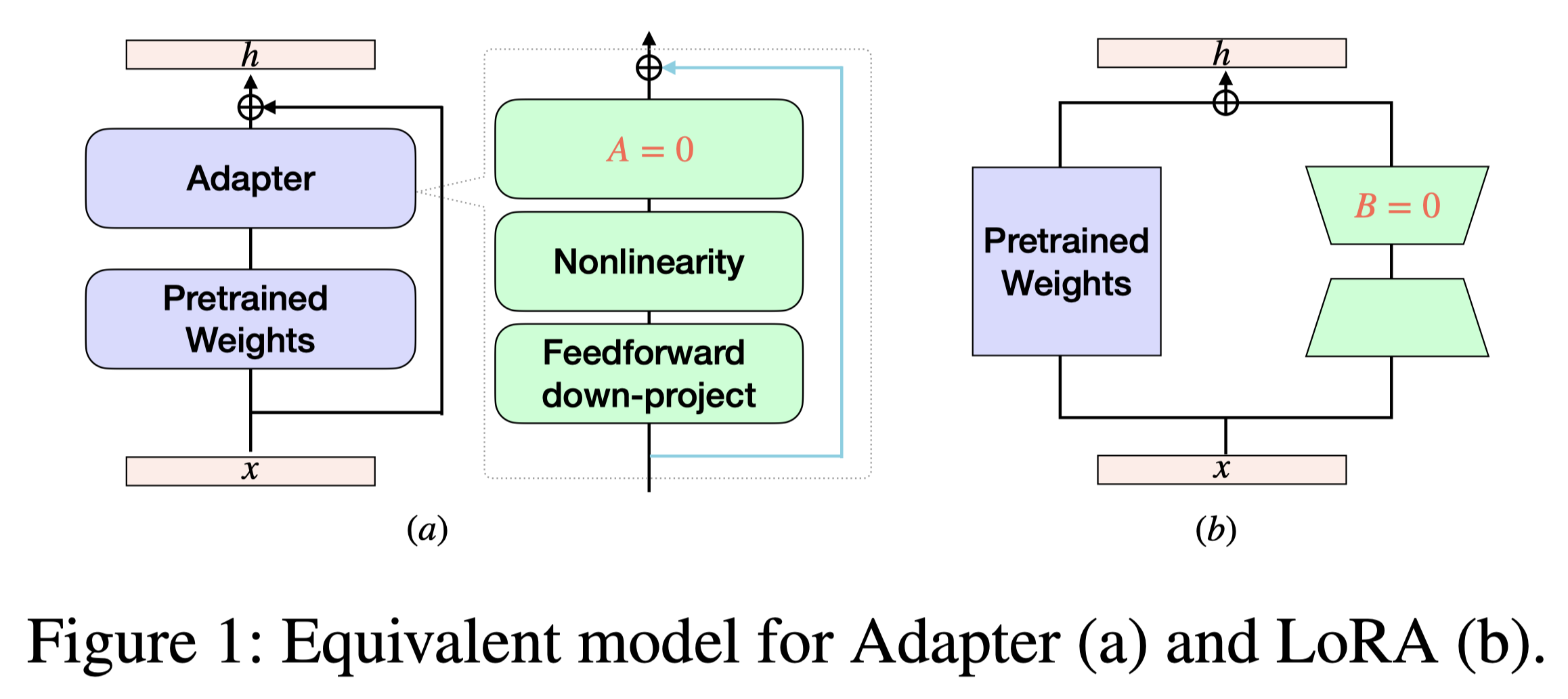
The Adapter [5] model proposes to add an adapter layer inside the transformer layer. While this alters the original model’s structure, the Adapter model can be viewed as fine-tuning an equivalent model which initializes the matrix AA as an all-zero matrix. This equivalent model has the same output as the original pre-trained model for any input, while the structure is the same as the Adapter model. Therefore, fine-tuning the Adapter model can be viewed as fine-tuning partial parameters of the equivalent model with the same structure, making it a sparse fine-tuned model with respect to the equivalent model.

The LoRA [6] model proposes to add a new vector calculated by recovering a hidden vector from a lower dimension space. The original initialization makes the LoRA model an equivalent model for the original pre-trained model as the matrix BB is set to 0. Therefore, fine-tuning a LoRA model can also be viewed as fine-tuning partial parameters of the equivalent model with the same structure, making it a sparse fine-tuned model as well.

adapterandlora

Projection-Based Approaches

Projection-based approaches, such as DiffPruning and ChildPruning, utilize task-specific data to select tunable parameters.

The DiffPruning [7] model proposes to model the parameter selection mask as a Bernoulli random variable and optimize the variable with a reparametrization method. It then projects the mask onto MM’s feasible region and performs the optimization alternately. Therefore, it also aligns with the definition of a sparse fine-tuned model.

The ChildPruning [8] model proposes to iteratively train the full model parameters and then calculates the projected mask to find the child network. This approach of alternating between full model training and mask projection also complies with the definition of a sparse fine-tuned model.

In Conclusion

The sparse fine-tuned model provides a unified view of various parameter-efficient models. By adhering to the definition of a sparse fine-tuned model, these models can achieve efficient usage of parameters during fine-tuning, leading to more effective and resource-friendly machine learning models. For a more comprehensive understanding of this concept, kindly refer to the original paper, On the effectiveness of parameter-efficient fine-tuning[1:2], or visit the corresponding Github Homepage.

  1. Fu, Z., Yang, H., So, A. M., Lam, W., Bing, L., & Collier, N. (2023). On the effectiveness of parameter-efficient fine-tuning. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 37, No. 11, pp. 12799-12807). ↩︎ ↩︎ ↩︎

  2. Lee, C., Cho, K., & Kang, W. (2019). Mixout: Effective Regularization to Finetune Large-scale Pretrained Language Models. In International Conference on Learning Representations. ↩︎

  3. Zaken, E. B., Ravfogel, S., & Goldberg, Y. (2021). Bitfit: Simple parameter-efficient fine-tuning for transformer-based masked language-models. arXiv preprint arXiv:2106.10199. ↩︎

  4. Han, S., Mao, H., & Dally, W. J. (2015). Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv preprint arXiv:1510.00149. ↩︎

  5. Houlsby, N., Giurgiu, A., Jastrzebski, S., Morrone, B., De Laroussilhe, Q., Gesmundo, A., Attariyan, M., & Gelly, S. (2019). Parameter-efficient transfer learning for NLP. In International Conference on Machine Learning (pp. 2790-2799). PMLR. ↩︎

  6. Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., Wang, L., & Chen, W. (2022). LoRA: Low-Rank Adaptation of Large Language Models. In International Conference on Learning Representations. ↩︎

  7. Guo, D., Rush, A. M., & Kim, Y. (2021). Parameter-Efficient Transfer Learning with Diff Pruning. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers) (pp. 4884-4896). ↩︎

  8. Xu, R., Luo, F., Zhang, Z., Tan, C., Chang, B., Huang, S., & Huang, F. (2021). Raise a Child in Large Language Model: Towards Effective and Generalizable Fine-tuning. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing (pp. 9514-9528). ↩︎