切问录

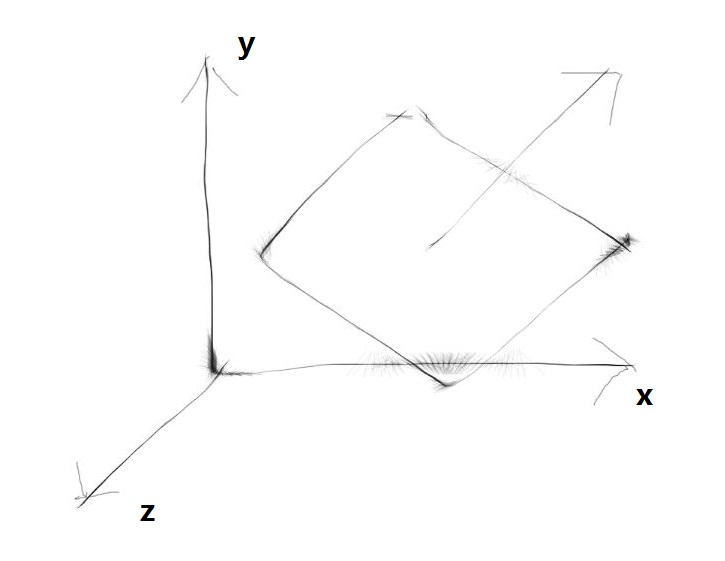
在曲面积分中，有向面元 $d\mathbf{S}= \mathbf{n}dS=(dydz,dzdx,dxdy)$。
那么这个结论的几何意义如何理解？
如图，法向量$\mathbf{n}$在$x$方向上的投影越长，就说明通过$yz$平面的向量越多。也就是说$n_x$和$dydz$有某种对应关系。这个关系就是$n_xdS=dydz$

拉格朗日方程式理论力学中非常重要的一个方程，它的出现标志着分析力学的诞生，比起传统的牛顿定律来用拉格朗日方程能求解更多的广义坐标系统，且拉格朗日方程能直接导出牛顿运动定律。除此之外，隐藏在这个方程背后的变分思想却更值得我们关注。本文描述了利用变分法推导拉格朗日方程的过程。

拉格朗日方程的出发点是：当一个系统是真实存在的情况下如下泛函$J$取极值亦即$\delta J=0$

$$J=\int_a^bF(x,y,y')dx$$

在后续的推导过程中，注意到：

1. 变分运算和微分运算差不多，$J$的变分

$$\delta J=\frac{\partial J}{\partial u_i}\delta u_i$$

2. 对$y$变分的时候，与$x$无关。

3. $\delta$和$d$可以直接交换顺序，即 $\delta dy=d\delta y$

4. $y$的变分满足关系

$$\begin{cases}\delta y(a)=0\\\delta y(b)=0\end{cases}$$

因此$J$的变分可表示为：

\begin{align} \delta J&=\int_a^b(F_y\delta y+F_{y'}\delta y')dx \\ &=\int_a^b F_y\delta y dx+\int_a^b F_{y'}\delta y' dx \\ &=\int_a^b F_y\delta y dx+\int_a^b F_{y'}\delta dy \\ &=\int_a^b F_y\delta y dx+ F_{y'}\delta y \big|_a^b - \int_a^b \delta y dF_{y'} \\ &=\int_a^b F_y\delta y dx - \int_a^b \delta y \frac{dF_{y'}}{dx}dx\\ &=\int_a^b (F_y-\frac{dF_{y'}}{dx})\delta y x\end{align}

由变分法基本引理可知，要想让$\delta J$恒为0，只能是括号里面的项为0即：

$$F_y-\frac{dF_{y'}}{dx}=0$$

在数分中，我们学习了分部积分公式，而在处理多元微积分问题的时候，我们需要用到它的推广形式。下面先给出公式，随后给出该公式的证明，以及一个特殊情形。最后给出直观的一个解释。

$$\int_\Omega f\nabla \cdot \boldsymbol{A} d\Omega+ \int_\Omega \boldsymbol{A} \cdot \nabla f d\Omega=\int_S f \boldsymbol{A}d\boldsymbol{S}$$

证明如下：

设在空间中，存在向量场$\boldsymbol{B}$由高斯公式，有：

$$\int_\Omega \nabla\cdot\boldsymbol{B}d\Omega=\int_S \boldsymbol{B} d\boldsymbol{S}$$

令$\boldsymbol{B}=f\boldsymbol{A}$,带入得：

$$\int_\Omega \nabla\cdot f\boldsymbol{A}d\Omega=\int_S f\boldsymbol{A} d\boldsymbol{S}$$

$$\int_\Omega f \nabla\cdot \boldsymbol{A} d\Omega+\int_S \boldsymbol{A} \cdot\nabla f d \Omega=\int_S f\boldsymbol{A} d\boldsymbol{S}$$

特殊地，只考虑$\boldsymbol{A}$的一个分量（设为g），原式变为：

$$\int_\Omega f \nabla g d\Omega=\int_S fgd\boldsymbol{S}-\int_\Omega g\nabla f d\Omega$$

这个公式让我们看到，分部积分就是将被积函数的求导项和未求导项交换，然后用两个函数（都不求导）在表面上的积分去减它就行。回想起一元函数定积分分部积分公式，最前面写的是$f(x)g(x)\big|_a^b$的形式，之所以这个地方要用$f(b)g(b)-f(a)g(a)$，是因为“表面”只有两个点，且法向量方向相反。

天下大事，分久必合，合久必分。这是《三国演义》的开篇之语，更是恰当地概括了中国古代历史形式。总的来看，中国分分合合，而整个民族亦在这种分与合生生不息。那么中国为什么有分分合合？

结论是：一个政权之建立，必有一种与之相应的光明的思想为其支柱。如果这个思想暗淡了，政权的寿命亦必不可久，而分裂之势亦不能避免。
先来看看战国时期，也就是那个人才辈出百花齐放的年代。诸子百家，交相辉映，来向世人解释着我们这个世界。西方人解决了人和物的关系，印度人解决了人和神的关系，而中国人解决了人和人的关系。而诸子百家解释的这个人与人的关系，却稍有不同。要之如下：

这篇文章主要介绍度量张量的起源及它的基本应用。张量是19世纪以来比较伟大的数学发明之一，它的发明伴随着微分几何的提出，为在流形上进行各种运算提供了可能。在这里主要讲解度量张量。首先我们来看一看我们需要解决一个什么问题，然后针对这个问题提出一种新的解决思路，最后讲解度量张量的使用。

一、问题提出

在物理学中，经常使用到内积运算，比如求一个力所做的功，我们有：

$$W=\vec{F}\cdot\vec{S}$$

这个公式很简单，计算的时候将$\vec{F}$和$\vec{S}$的各个分量乘起来再相加即等于内积。但是如果$\vec{F}$和$\vec{S}$定义在其他坐标系（如非正交的坐标系）下，那么直接用各个分量乘起来再相加得出的功就会有所不同！而根据我们的常识，功应该和坐标系的选择无关，也就是说，两个向量的内积是与坐标无关的，我们可以猜想点乘或许在某种情况下不等于内积。那么我们就需要引入一种对内积的新的认识。本文即将讨论如何用点乘在所有坐标系下表示出内积，这种表示中就用到了度量张量。

二、解决思路

为了解决这个问题，我们先引入几个基本概念，首先是爱因斯坦求和约定，其次是克罗内克符号，最后是逆变坐标和协变坐标。

2.1爱因斯坦求和约定

我们定义:
$$a_i b_i=\sum\limits_{i=1}^{n}a_i\cdot b_i$$
$$a_{ij} b_j=\sum\limits_{j=1}^{n}a_{ij}\cdot b_j$$

终于，在biz.nf上的免费空间挂掉了。作为一个程序员，终于决定将博客搬到github上。等配置完成我会将这个过程记录下来。
在此测试一下效果：

这是一句引用

测试一下$\LaTeX$:

$$\int_\Omega \nabla f d\omega=0$$

code:

1
2
3

for i in 10:
    if a>0:
        a = 0