参考文献

[1] 概率与数理统计 陈希孺

1
2
3
4
5
6
7
8
9

url: http://fuzihao.org/blog
root: /blog/

........

deploy:
  type: git
  repo: https://github.com/maplewizard/blog.git
  branch: gh-pages

完成设置后，打开github新建一个名为blog的仓库，并将刚才设置好的内容部署到这上面，即www.fuzihao.org/blog。

org-mode 入门教程

org-mode是Emacs提供的一个强大的编辑模式，可以用于做会议笔记以及制作各种待办事项（GDT）。其语法类似于Markdown但是提供了比Markdown更多的操作，再加上Emacs强大的编辑功能，能给笔记增加很多动态的操作（能纯文本上实现折叠、展开、树状视图、表格求和、求代码运行结果等功能），可以说org-mode是最强大的标记语言。而org-mode的强大，也导致了他比markdown更加复杂，需要花些时间来练习，本文选出了org-mode最强大、实用的功能，进行最简单的介绍，下面介绍org-mode的使用方法。

安装

Emacs最新版本（24.4）自带org-mode，这就意味着只要打开一个后缀名为org的文件就会自动进入org-mode。因此我们只需要下载最新版的Emacs即可。
　　
windows用户：到http://ftp.gnu.org/gnu/emacs/windows/ 下载最新版
ubuntu系列：在终端中输入：sudo apt-get install emacs

配置

org-mode功能基本比较完善，不需要更多的配置，但是org模式下默认没有自动换行的功能，我们在.emacs文件里面添加如下代码，实现自动换行：

(add-hook 'org-mode-hook (lambda () (setq truncate-lines nil)))

实例教程

以下分别讲解org-mode下几个实用的功能，更完整的教程可以参考官网教程。下面一步一步完成我们的org文件。（本教程中我们定义 C-x 表示按Ctrl+x，M+x标识Alt+x，S+x代表Shift+x，这也是Emacs的标准定义）

新建文件

1. 打开Emacs
2. 输入 C-x C-f ～/test/test.org

我们在之前研究过两个随机变量的独立性，我们定义若两个随机变量$X,Y$满足

$$P(X,Y)=P(X)P(Y)$$

则我们说随机变量$X,Y$独立。下面来直观地理解这个公式，可以发现，如果$X,Y$独立，那么已知$X$，将不会对$Y$的分布产生任何影响，即是说$P(Y)=P(Y|X)$，这个结果的证明也很简单，由贝叶斯公式：

$$P(Y|X)=\frac{P(X,Y)}{P(X)}=\frac{P(X)P(Y)}{P(X)}=P(Y)$$

即证。

由此可以看出，独立性反应了已知$X$的情况下，$Y$的分布是否会改变，或者说，在给定随机变量$X$之后，能否为$Y$带来额外的信息。然而独立性只能表示出两个随机变量之间是否会有关系，但是却不能刻画他们的关系大小。下面我们引入互信息，它不仅能说明两个随机变量之间是否有关系，也能反应他们之间关系的强弱。我们定义互信息$I(X,Y)$：

$$I(X;Y)=\int_X \int_Y P(X,Y)\log\frac{P(X,Y)}{P(X)P(Y)}$$

我们来稍微理解一下，log里面就是$X,Y$的联合分布和边际分布的比值，如果对所有$X,Y$，该值等于1，即是说他们独立的情况下，互信息$I(X;Y)=0$，即是说这两个随机变量引入其中一个，并不能对另一个带来任何信息，下面我们来稍稍对该式做一个变形

$$\begin{aligned} I(X;Y)&=\int_X \int_Y P(X,Y)\log\frac{P(X,Y)}{P(X)P(Y)}\\ &=\int_X \int_Y P(X,Y)\log\frac{P(X,Y)}{P(X)}-\int_X \int_Y P(X,Y)\log{P(Y)}\\ &=\int_X \int_Y P(X)P(Y|X)\log P(Y|X) -\int_Y \log{P(Y)}\int_X P(X,Y)\\ &=\int_X P(X)\int_Y P(Y|X)\log P(Y|X)-\int_Y \log{P(Y)}P(Y)\\ &=-\int_X P(X)H(Y|X=x)+H(Y)\\ &=H(Y)-H(Y|X)\\ \end{aligned}$$

其中，$H(Y)$是$Y$的熵，定义为

$$H(Y)=-\int_Y P(Y)\log{P(Y)}$$

衡量的是$Y$的不确定度，即使说，$Y$分布得越离散，$H(Y)$的值越高，而$H(Y|X)$则表示在已知$X$的情况下，$Y$的不确定度，而$I(X;Y)$则表示由$X$引入而使$Y$的不确定度减小的量，因而如果$X,Y$关系越密切，$I(X;Y)$越大，$I(X;Y)$最大的取值是$H(Y)$，也就是说，$X,Y$完全相关，由于X的引入，$Y$的熵由原来的$H(Y)$减小了$I(X;Y)=H(Y)$，变成了0，也就是说如果$X$确定，那么$Y$就完全确定了。而当$X,Y$独立时，$I(X;Y)=0$引入$X$，并未给$Y$的确定带来任何好处。

总结下$I(X;Y)$的性质：
1）$I(X;Y)\geqslant 0$
2）$H(X)-H(X|Y)=I(X;Y)=I(Y;X)=H(Y)-H(Y|X)$
3）当$X,Y$独立时，$I(X;Y)=0$
4）当$X,Y$知道一个就能推断另一个时，$I(X;Y)=H(X)=H(Y)$

仿射空间与仿射变换在计算机图形学中有着很重要的应用。在线性空间中，我们用矩阵乘向量的方法，可以表示各式各样的线性变换，完成诸多的功能，但是有一种极其常用的变换却不能用线性变换的方式表示，那就是平移，一个图形的平移是非线性的！（这一点只需要看平移前各点与原点的连线和平移后各点与原点之间的连线可知，或者记平移变换为$\mathcal{F}$，有$\mathcal{F}(\boldsymbol{v_1}+\boldsymbol{v_2})\not =\mathcal{F}(\boldsymbol{v_1})+\mathcal{F}(\boldsymbol{v_2}))$

放射空间与仿射组合

为了用数学的方式来描述这种变换，就需要用到仿射变换（平移不是线性变换而是仿射变换）。下面先讲仿射空间。形象地来讲，仿射空间就是没有原点的线性空间。在线性空间中，两个点相加，可以定义为原点到两个点的向量线性相加，而在仿射空间中，由于没有原点，因此不能定义相加，没有线性组合。但我们可以定义一个仿射组合来用若干基表出某个点。我们定义仿射组合：

$$\boldsymbol{p}=\sum_{i=1}^N \lambda_i \boldsymbol{v_i}\quad\quad(\sum_{i=1}^N \lambda_i=1)$$

我们不妨在线性空间中来看这个式子，假设就两个向量$\boldsymbol{v_1,v_2}$我们任意指定一个原点$\boldsymbol{q}$，设$\boldsymbol{v_1}$的系数为$\lambda$，则$\boldsymbol{v_2}$的系数为$1-\lambda$，那么$\boldsymbol{p}=\boldsymbol{q}+\lambda(\boldsymbol{v_1}-\boldsymbol{q})+(1-\lambda)(\boldsymbol{v_2}-\boldsymbol{q})=\lambda \boldsymbol{v_1}+(1-\lambda)(\boldsymbol{v_2})$。通过推导，原点$\boldsymbol{q}$被消去了，也就是说，仿射组合跟原点的选择没有任何关系！

仿射变换

有了仿射组合，就可以仿照线性组合来定义仿射变换：

给定两个仿射空间$\mathcal{A},\mathcal{B}$，一个函数$f:\mathcal{A}\rightarrow \mathcal{B}$是仿射变换，当且仅当对仿射组合

\sum_{i=1}^N \lambda_i \boldsymbol{v_i}\quad\quad(\sum_{i=1}^N \lambda_i=1)$$都有 $$f(\sum_{i=1}^N \lambda_i \boldsymbol{v_i})=\sum_{i=1}^N \lambda_if(\boldsymbol{v_i})\quad\quad(\sum_{i=1}^N \lambda_i=1)

这种系数又叫质心坐标，哪个点的系数大，就相当于质量大，质心就离那个点近。仿射变换得到的结果就是给定点按质量加权的质心，质心的仿射变换等于每个点进行放射变换后再求质心。

用线性变换表示仿射变换

下面来看如何表示仿射变换，我们定义$\mathbb{R}^n$中一个向量$\boldsymbol{v}$的齐次形式为$\mathbb{R}^{n+1}$中的$\overset{\sim}{\boldsymbol{v}}=\left[\begin{aligned}\boldsymbol{v} \\ 1\end{aligned}\right]$那么，仿射组合与系数和为1的要求可统一表示为

$$\left[\begin{aligned}\boldsymbol{y} \\ 1\end{aligned}\right]=c_1\left[\begin{aligned}\boldsymbol{v_1} \\ 1\end{aligned}\right]+c_2\left[\begin{aligned}\boldsymbol{v_2} \\ 1\end{aligned}\right]+\cdots+c_n\left[\begin{aligned}\boldsymbol{v_n} \\ 1\end{aligned}\right]$$

也就是说，仿射组合可以写成高一维对应齐次坐标的线性组合形式。那么对于一个附加平移的变换

$$\boldsymbol{y}=A\boldsymbol{x}+\boldsymbol{b}$$

我们可以将其改写成其次坐标的形式

\left[\begin{aligned}\boldsymbol{y} \\ 1\end{aligned}\right]=\left[\begin{aligned}&A &\boldsymbol{b} \\ &0 &1\end{aligned}\right]\cdot\left[\begin{aligned}\boldsymbol{x} \\ 1\end{aligned}\right]$$这也是在计算机图形学中对平移的处理方式。下面一个摘自维基百科的图形象地说明了这一过程 <center>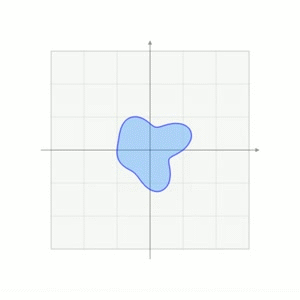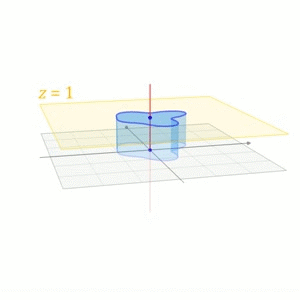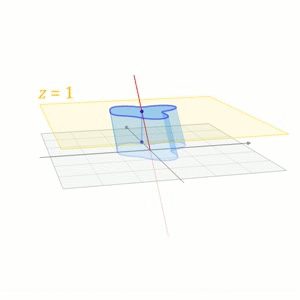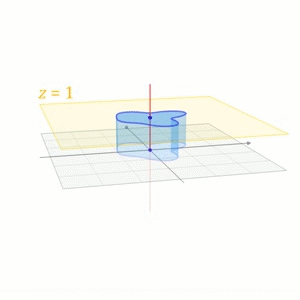</center> 　　　　　　　　　　 ## 其它 　　我们再来看看质心坐标（Barycentric Coordinates），采用质心坐标的好处在于它能够表示每一点受周围点的影响，质心坐标的系数越大，影响越大，因此在线性插值时，可以直接用质心坐标来乘以每一点的值，得出的就是插值后的结果，在计算机图形学中进行渲染时，颜色差值就用这种算法。 　　　　　　　　　　　　　　　　　　 ## 参考文献 [1]D C.Clay Linear Algebra and its application 4th edition [2]http://en.wikipedia.org/wiki/Affine_space [3]http://en.wikipedia.org/wiki/Affine_transformation

网页中大部分的限制都是由js编写的，而chrome提供了一个修改js代码的工具，利用这个工具可以轻松解决各种时间等待之类的限制。本文主要通过利用chrome命令行修改变量值得方式，控制运行流程。

sigmoid函数

sigmoid函数定义为

$$g(z)=\frac{1}{1+e^{-z}}$$

对于一般的模型，通常有$z=\theta^{\mathrm{T}}x$，可以看做是样本各属性的加权。sigmoid函数求导有$g'(z)=g(z)(1-g(z))$，这个在神经网络推导的时候会用到。

Logistic回归

Logistic回归是针对二分类问题常用的一种回归，其回归模型为：

$$h_\theta(x)=\frac{1}{1+e^{-\theta^{\mathrm{T}}x}}$$

其中$x$是某个样本的属性向量，$\theta$是参数向量。在用Logistic回归时，需要找到合适的参数$\theta$，使得能量函数（误差）$J(\theta)$最小，在使用梯度下降法更新参数$\theta$的更新过程中需要使用到梯度，然后在每一步执行$\theta:=\theta-\alpha\nabla_\theta J(\theta)$，其中$\alpha$是学习速度，能量函数被定义为：

$$J(\theta)=-\frac{1}{m}\sum_{i=1}^m\left[y^{(i)}\log h_{\theta}(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta}(x^{(i)}))\right]$$

其中

$$h_{\theta}(x^{(i)})=\frac{1}{1+e^{-\theta^{\mathrm{T}}x^{(i)}}}$$

下面来给出其梯度的推导

$\mathcal{Everything~should~be~made~as~simple~as~possible,~but~not~ simpler.}$

$--\mathcal{Albert\quad Einstein}$

\begin{align} E&=\int_0^xFdx =\int_0^x\frac{d}{dt}(mv)dx =\int_0^t\frac{d}{dt}(mv)vdt =\int_0^{mv}vd(mv) =\int_0^v vd\left(\frac{m_0v}{\sqrt{1-(v/c)^2}}\right)\\ &=m_0\int_0^v\left(\frac{v}{[1-(v/c)^2]^{1/2}}+\frac{v^3/c^2}{[1-(v/c)^2]^{3/2}}\right)dv =m_0\int_0^v\frac{vdv}{[1-(v/c)^2]^{3/2}}\\ &=m_0c^2\left(\frac{1}{[1-(v/c)^2]^{1/2}}-1\right) =(mc^2-m_0c^2) =(m-m_0)c^2\Rightarrow \end{align}

$$E=mc^2$$