切问录

By Z.H. Fu https://fuzihaofzh.github.io/blog/ ### 几种必考虑的情况 - 只要有除法，就一定要讨论分母为0； - 一定要判断函数输入参数是否合法； - 指针使用时判断是否非0，用完了置为0。

函数压栈顺序

从右往左。
所以

int g = 1;
printf("%d, %d", g, ++g);

结果为2,2

int g = 1;
printf("%d, %d", g, g++);

结果为2,1，说明g++.exe是解析一个参数就加一次，不是解析完一行再加。

条件解析顺序

从左往右，如果当前已经足以判断（&&前面是False或||前面是True），则不会计算后续条件。

boolalpha

函数名称，功能是把bool值显示为true或false。

cout << boolalpha << ( str1==str2 ) << endl;

(int &)

float a = 1.0f
cout<<(int &)a
从a的起始地址开始，读取sizeof(int)长度，当整数输出

By Z.H. Fu https://fuzihaofzh.github.io/blog/ 　　今天重新研究了下拉普拉斯变换，很多资料只是给出了其公式，并没有给出其来历，特别是那个$s$的出现显得非常莫名其妙。本文旨在给出拉普拉斯变换的一个直观上的理解，对严谨性不做保证。 　　我们在研究很多数学问题的时候，特别是一些复杂的问题的时候，无法直接入手，而是将问题分解到许多维度上去，在这些简单的维度去进行处理，因此我们有了泰勒展开，有了幂级数、傅里叶级数，我们将傅里叶技级数再往连续域上推广，又有了傅里叶变换。而拉普拉斯变换，可以从幂级数的概念中推广出来，下面给出其推广过程。 一个函数可以用幂级数的形式表出： $$A(x)=\sum_{i=1}^\infty a_ix^i$$ 我们可以看出，构造一个函数$A(x)$的过程，我们输入了一个序列$\{a_1,a_2,\cdots\}$，输出了一个函数$A(x)$，（这个地方的$x$是输出的函数的自变量，和拉普拉斯变换的定义还稍有不同，我们一会来解决这个问题），其实这个序列可以看成是一个特殊的函数，即自变量只取整数的函数，那么我们将其推广为一般函数会有什么效果？将离散自变量$i$用连续自变量$t$代替，求和推广为积分，我们有： $$A(x)=\int_0^{+\infty} f(t)x^tdt$$ 而在微积分中，我们常常引入自然指数来方便运算，有： $$\begin{aligned}A(x)&=\int_0^{+\infty} f(t)x^tdt\\ &=\int_0^{+\infty} f(t)(e^{\ln x})^tdt \end{aligned}$$ 在这里，我们需要对$x$做一些限定，因为幂级数存在收敛半径的，对于一般的自然界中存在的实际函数（如信号）是不能发散到正无穷的，因此该函数有上界，因而，对于$x\lt 1$的幂级数一定收敛（可以用$\sqrt[n]{a_n}$那个半径判据），即幂级数收敛半径为1，而由于为了避免负的幂带来的困扰，我们要求$x\gt 0$。由于$0\lt x \lt 1$，而$\ln x \in (-\infty,0)$。也就是说，这样我们得到的变换的函数对其自变量的范围有所限制，为$x \in (0,1)$，这当然很不好看，因此我们做一个代换，令 $$-s=\ln x$$ 将$A(x)$用$F(x)$代替，因此原始变为 $$F(x)=\int_0^{+\infty}f(t)e^{-st}dt\quad s \in(0,+\infty)$$ 这正是拉普拉斯变换！ 　　注意了，这里，我们变换后的函数本来是$F(x),x\in(0,1)$，但是，这种形式很难看，在操作时也很麻烦，因此我们做了变量代换，得到了变换后的函数$F(s),s\in(0,+\infty)$两个其实是一回事。将拉普拉斯变换用符号$\mathcal{L}$表示，记作： $$\mathcal{L}(f(t))=F(s)$$

参考文献：
[1] 微分方程公开课.Massachusetts Institute of Technology.Arthur Mattuck

By Z.H. Fu https://fuzihaofzh.github.io/blog/ 　　以前上高中的时候问过数学老师这个问题，被老师骂了一顿，说这是规定，后来也就没太在意。今天看了Stanford Andrew Ng讲的《机器学习》，明白了为什么最小二乘法对误差的估计要用平方，而不是绝对值或是四次方。

简单地说，之所以要用这种规定，是因为，取二次方的时候，对参数的估计是当前样本下的最大似然估计。下面给出证明。

记样本为$(x^{(i)},y^{(i)})$，对样本的预测为$\hat y^{(i)}|_\boldsymbol{\theta}$该记法表示该预测依赖于参数$\boldsymbol{\theta}$的选取。我们有：
　　$$\boldsymbol{y}=\boldsymbol{\hat y|\theta}+\boldsymbol{\epsilon}$$
　　其中，$\boldsymbol{\epsilon}$是一个误差函数，我们通常认为其服从正态分布即
　　$$\boldsymbol{\epsilon }\sim N(0,\sigma^2)$$
因此有
　　$$\begin{aligned}\boldsymbol{y}-\boldsymbol{\hat y|\theta}&\sim N(0,\sigma^2)\ \boldsymbol{y}&\sim N(\boldsymbol{\hat y|_\boldsymbol{\theta}},\sigma^2)\end{aligned}$$
要求$\boldsymbol{\theta}$的极大似然估计，即是说，我们现在得到的这个真实存在的$\boldsymbol{y}$在$\boldsymbol{\theta}$不同的取值下，出现概率最大，我们来看这个概率。令

$$L(\boldsymbol{\theta})=P(\boldsymbol{y}|\boldsymbol{x};\boldsymbol{\theta})=\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)}-\hat y^{(i)}|_\boldsymbol{\theta})^2}{2\sigma})$$

为了简化计算，令

$$\begin{aligned}l(\boldsymbol{\theta})&=\log L(\boldsymbol{\theta})\\&=m\log \frac{1}{\sqrt{2\pi}}+\sum_{i=0}^m-\frac{(y^{(i)}-\hat y^{(i)}|_\boldsymbol{\theta})^2}{2\sigma}\end{aligned}$$

要让$L(\boldsymbol{\theta})$最大，即需让$l(\boldsymbol{\theta})$最大，即让$\sum_{i=0}^m(y^{(i)}-\hat y^{(i)}|_\boldsymbol{\theta})^2$取到最小值。

综上，当误差函数定为平方时，参数$\boldsymbol{\theta}$是样本的极大似然估计。

By Z.H. Fu https://fuzihaofzh.github.io/blog/ 最近学习线性代数的有关东西，在看到奇异值分解（svd）时，发现了一个在图像压缩上的应用。 奇异值分解：在线性代数中，我们知道对任意一个矩阵都存在奇异值分解，$\boldsymbol{A}=\boldsymbol{U\Sigma V^\mathrm{T}}$，其中$\boldsymbol{U}$和$\boldsymbol{V}$是标准正交矩阵，而$\boldsymbol{\Sigma}$是一个对角矩阵，每一个对角元是该矩阵的一个奇异值，奇异值指的是矩阵的特征值开根号。其具体分解形式如下： $$ \boldsymbol{A}=\begin{bmatrix}u_1 &u_2 &\cdots &u_m\end{bmatrix}\begin{bmatrix}\boldsymbol{D} & \boldsymbol{0} \\\boldsymbol{0} &\boldsymbol{0}\end{bmatrix}\begin{bmatrix}v_1^\mathrm{T}\\ v_2^\mathrm{T} \\ \vdots \\ u_n^\mathrm{T}\end{bmatrix} $$ 其中 $$\boldsymbol{D}=\begin{bmatrix} \sigma_1 &0 &\cdots &0 \\ 0 & \sigma_2 &\vdots &0 \\ \vdots &\vdots &\ddots &\vdots \\ 0 &0 &\cdots &\sigma_r\end{bmatrix}$$ 将$\boldsymbol{A}$展开得 $$\boldsymbol{A}=\sigma_1\boldsymbol{u_1v_1^\mathrm{T}}+\sigma_2\boldsymbol{u_2v_2^\mathrm{T}}+\cdots+\sigma_r\boldsymbol{u_rv_r^\mathrm{T}}$$ 将$\boldsymbol{A}$看成一个图像的矩阵，上面和式的每一个分量按大小排序，越大，说明越重要。而后面的权很小，可以舍去，如果只取前面k项，则数据量为$(m+n+1)k\ll mn$因而达到了压缩图像的目的。 通过对比发现，当$k=\frac{r}{20} $时，能基本看清图像。当$k=\frac{r}{4} $时基本看不出任何区别，对于长宽相等的图像，此时数据量占原数据量的$k=\frac{2k}{n} $,在测试图像中，这个数值为0.5 。可见图像压缩的效果是显著的。 处理结果如下： 原始图像：  k=1:  k=2:

By Z.H. Fu https://fuzihaofzh.github.io/blog/

这是一年前做的一个小算法，今天把它搬运过来。该算法的主要目的是利用灰度形态学腐蚀对3D点云进行曲面重建。
给定点云的数据文件（这是美国卫星的数据，能在官网上下载到），寻找一种方法，重建原来的曲面。点云数据为卫星扫描的las文件。
点云数据：

 原始点云  处理后的效果

由于是卫星得到的数据，因此可以发现数据点基本都是楼房的屋顶。
而他的平面视图如下：

by Z.H. Fu https://fuzihaofzh.github.io/blog/

此书成于民族危难之际，于仓促流亡中作成，然则艰苦的条件却未能影响此书之博大，作者识解之渊博、见地之透彻，纵使七十年后翻看此书，亦多能得其教益。作者作书本意，或在加强国民信心，增强国民的凝聚力，故而字里行间，无不透露着一种对历史的温情与敬意。历史得失，即在今日，故不乏其可叹之事，亦颇有其可鉴之处。若议废封建、魏晋官制、北朝改革、安石变法，其事或成或败，其议或褒或贬，观其是非而览其得失，亦多于吾辈切己修身处，多有所教言，故以其要略而录于是。

[TOC]

对于国史之信念

一、当信任何一国之国民，尤其是自称知识在水平线以上之国民，对其本国已往历史，应该略有所知。(否则最多只算一有知识的人，不能算一有知识的国民。)
　　二、所谓对其本国已往历史略有所知者，尤必附随一种对其本国已往历史之温情与敬意。(否则只算知道了一些外国史，不得云对本国史有知识。)
　　三、所谓对其本国已往历史有一种温情与敬意者，至少不会对其本国历史抱一种偏激的虚无主义，(即视本国已往历史为无一点有价值，亦无一处足以使彼满意。)亦至少不会感到现在我们是站在已往历史最高之顶点，(此乃一种浅薄狂妄的进化观。)而将我们当身种种罪恶与弱点，一切诿卸于古人。(此乃一种似是而非之文化自谴。)
　　四、当信每一国家必待其国民具备上列诸条件者比较渐多，其国家乃再有向前发展之希望。(否则其所改进，等于一个被征服国或次殖民地之改进，对其自身国家不发生关系。换言之，此种改进，无异是一种变相的文化征服，乃其文化自身之萎缩与消灭，并非其文化自身之转变与发皇。)

By Z.H. Fu https://fuzihaofzh.github.io/blog/ 　　拉格朗日乘数法在优化理论中起着非常重要的作用。本文将给出拉格朗日乘数法的具体步骤和一个直观的理解。

拉格朗日乘数法解决这样一个问题：
　　
　　$$\begin{cases}maximize\quad &f(x,y) \ subject \quad to\quad &g(x,y)=c\end{cases}$$
　　我们在等高线图上考虑，先任取$f(x,y)=d_2$此时，等高线与约束线的交点既是满足约束且取值为$d_2$的点。下面，我们逐渐增大$f(x,y)$的取值，即$d$逐渐由$d_2$变为$d_1$，这个过程中，$f(x,y)$的值逐渐增大，当达到$d_1$后，再增大一点点，即不满足约束，因此$d_1$既是$f(x,y)$在该约束下的最大值。而这个时候，约束曲线正好和等高线相切。既是说，在这一点，$f(x,y)$和$g(x,y)$的梯度方向相同，拉格朗日乘数法即是刻画了梯度方向相同这一特点。我们能找到一个标量$\lambda$使得：　　$$\nabla f+\lambda \nabla g=0 $$
　　
　　以下给出更规范的描述。
　　令拉格朗日函数
　　$$\Lambda(x,y,\lambda)=f(x,y)+\lambda (g(x,y)-c)$$
　　优化问题取得最大值，等价于拉格朗日函数取得驻点。即：
　　$$\nabla_{x,y,\lambda}\Lambda=0$$
　　这样，就将一个带约束优化问题，转化成了一个无约束的极值问题。

参考文献

[1]拉格朗日乘数 https://zh.wikipedia.org/wiki/拉格朗日乘数

[2]Lagrange multiplier https://en.wikipedia.org/wiki/Lagrange_multiplier

By Z.H. Fu https://fuzihaofzh.github.io/blog/ 　　因为需要用FFD（Free Form Deformation）故而今天又学习了一下Bernstein多项式。现在将笔记记录如下。

首先给出Bernstein多项式：
　　$$b_{\nu,n}(x)=\binom{n}{\nu}x^\nu(1-x){n-\nu},\nu=0,…,n.$$
　　其中$x\in[a,b],\binom{n}{\nu}$是二项式系数。

我们再来回顾一下Bernstein多项式产生的历史。Bernstein多项式曾经被用来证明威尔斯特拉斯逼近定理（Weierstrass approximation theorem）。这个定理的大概意思是说：在$[a,b]$区间上所有的连续函数都可以用多项式来逼近。而且收敛性很强，是一致收敛。也就是说，可以将函数写成若干个Bernstein多项式相加的形式，而且，随着$n\rightarrow \infty$，该多项式将一致收敛到原函数！用表达式表示如下：
　　$$B_n(f)(x)=\sum^n_{\nu=0}f(\frac{\nu}{n})b_{\nu,n}(x)$$
　　其中$x\in[0,1]$,当$n\rightarrow \infty$时，该多项式收敛到原函数：
　　$$\lim_{n\rightarrow \infty}B_n(f)(x)=f(x)$$
　　好，我们发现这个跟傅里叶展开一模一样，所不同的是这里用的是多项式函数，Bernstein多项式在这里充当着基函数的角色。我们自然想到，能不能舍掉一些“高频分量”得到函数的大概形状？答案是显然的。我们选取若干个点，用这几个函数值来构造Bernstein多项式，得出的多项式就是一种“滤波”后的函数。

以下引出Bézier曲线。我们现在单纯地从基于分量的关系来看，我们有：
　　$$B_n(x)=\sum^n_{\nu=0}\beta_\nu b_{\nu,n}(x)$$
　　其中$\beta_\nu$是基函数的系数。将$\beta_\nu$取成一些点，我们有：
　　$$\mathbf{B_n(x)}=\sum^n_{\nu=0}\mathbf{P_\nu} b_{\nu,n}(x),x\in[0,1]$$
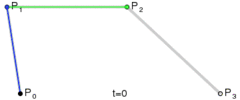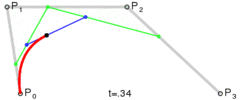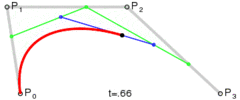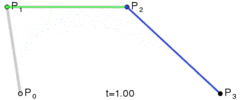
$\mathbf{P_\nu}$是我们给的点的坐标，而当$x$从0到1扫过时，我们就得到了一条曲线，这就是Bézier曲线。一个直观的图形如下：
　　
　　

参考文献：

Bernstein polynomial

https://en.wikipedia.org/wiki/Bernstein_polynomial

Bézier curve

https://en.wikipedia.org/wiki/Bézier_curve

By Z.H. Fu https://fuzihaofzh.github.io/blog/ 这是之前的一篇文章，方法是某天中午睡觉的时候突然梦到的。今天把它搬运过来。

利用线性代数的方法求斐波那契数列的通项
程序员们一定知道斐波那契数列的故事斐波那契数列指的是这样一个数列：1、1、2、3、5、8、13、21、34…… 这个数列从第三项开始，每一项都等于前两项之和。以前高中竞赛的时候或许人学习过特征方程来解这个问题，但当时也仅仅是会这种方法，到底是什么原理，还必须从线代的角度上来解释。
我们先来讲讲线性变换的概念怎么用于斐波那契数列。数列一项一项往前递推，就好像线性变换一次又一次地作用到一个向量上，那么作用n次后得到的向量中的某一项，就对应于数列的某一项。我们来看看具体的例子。对于斐波那契数列，我们有 $a_n=a_{n-1}+a_{n-2}$ 那么可以用矩阵的形式来表示这个变换：
我们首先通过前几项来找到变换矩阵$\mathbf{A}$

$$\left[ \begin{matrix} {a}_{2} \\ {a}_{3} \\ \end{matrix} \right]= \left[ \begin{matrix} ? & ? \\ ? & ? \\ \end{matrix} \right]\left[ \begin{matrix} {a}_{1} \\ {a}_{2} \\ \end{matrix} \right]$$

很明显，通过通项之间的关系可以看出：

$$\mathbf{A}=\left[ \begin{matrix} 0 & 1 \\ 1 & 1 \\ \end{matrix} \right]$$

令$\mathbf{x_n}=\left[ \begin{matrix}a_n \\ a_{n+1}\end{matrix} \right]$，那么我们根据这个递推关系，很容易得出:

By Z.H. Fu https://fuzihaofzh.github.io/blog/ 自从看了$\LaTeX$华丽的公式之后，就开始对office产生了质疑。毕竟，它的存储方式是它自己的格式，用其他的任何工具都无法编辑（有的话质量也不会很好）。因此，我们所有的文档都需要以一种纯文本的形式来保存。有了$\LaTeX$和MarkDown，这一理想终于得以实现。今天探索了一下如何使用$\LaTeX$制作ppt（当然，是pdf下的演示文档），现将过程和模板记录一下。

我们采用beamer来实现演示文档的功能，beamer是$\LaTeX$下最著名的一个演示文档的包，同时，我们将采用tikz来绘制流程图。
效果如下：